Programmeringskurs (alle) *: 3.2 while-løkker *
While-løkker
De første løkkene vi skal se på er while-løkker som skriver ut tallfølger.
En while-løkke lager vi slik:
while betingelse:
#\quad# handling
En while-løkke vil fortsette så lenge betingelsen er sann.
While-løkkene repeteres så lenge betingelsen er oppfylt, altså true. Det er først når betingelsen ikke er oppfylt, altså false, at programmet avslutter løkken og fortsetter videre i programmet. Med while-løkker kan vi derfor risikere at løkken aldri stopper, og at programmet vårt krasjer.
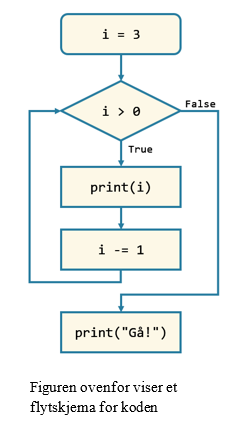
Nedenfor ser du en while-løkke som teller ned fra 3. Kjør programmet ved å trykke på ![]() .
.
Koden fungerer stegvis slik:
- Setter i lik 3.
- While-løkka starter.
- Koden spør: Er i (nå 3) større enn 0?
Siden dette er sant utføres koden i løkka.- Skriver ut i, altså 3.
- Trekker fra 1, slik at i = 2.
- Koden spør: Er i (nå 2) større enn 0?
Siden dette er sant utføres koden i løkka.- Skriver ut i, altså 2.
- Trekker fra 1, slik at i = 1.
- Koden spør: Er i (nå 1) større enn 0?
Siden dette er sant utføres koden i løkka.- Skriver ut i, altså 1.
- Trekker fra 1, slik at i = 0.
- Koden spør: Er i (nå 0) større enn 0?
Siden dette er feil avsluttes løkka, og fortsetter til neste linje i programmet.
- Koden spør: Er i (nå 3) større enn 0?
- Skriver ut «Gå!»
Merk at koden #\texttt{i -= 1}# gjør at variablen #\texttt{i}# minker med én for hver runde i løkken. Dersom vi ikke hadde hatt denne linjen ville programmet aldri stoppet, men skrevet ut uendelig mange 3-ere. Tilsvarende vil koden #\texttt{i += 1}# øke variabelen #\texttt{i}# med én.
a) Bruk en while-løkke til å skrive ut alle kvadrattallene som er mindre enn tallet 50.
b) Modifiser programmet i oppgave a slik at brukeren skal skrive inn et positivt heltall. Programmet skal så skrive ut alle kvadrattallene som er mindre enn dette.
LØSNING:
a) Her passer en while-løkke godt, for løkken skal skal gjentas så lenge tallet er mindre enn 50. Hvis k er kvadrattallet er betingelsen at #\texttt{k < 50}#
Kvadrattallene får vi ved å kvadrere, det vil si opphøye i andre. Derfor bruker vi en hjelpevariabel n som teller oppover fra 1, 2, 3 osv. Kvadrattallet k er da gitt ved #\textit{k = n}##^2#. Når løkken starter bør både n og k være lik 1.
For hver gang løkken repeteres skriver vi ut tallet før n økes med 1 og vi på nytt setter k lik #\textit{n}##^2#. Da blir koden slik:
b) Det er ikke store endringen som skal til for å få til dette. Vi oppretter bare en ny variabel, og bruker input for at brukerne skal bes om å skrive inn tallet. Denne variabelen bruker vi i betingelsen for whileløkka. Koden blir slik:

