Å finne nullpunkter til en funksjon er en viktig del av matematikken. Nå skal vi lære å finne nullpunkter ved å bruke kode. Vi tar utgangspunkt i funksjonen:

#f(x)=1,4x-4,9#

Du har sikkert lært å finne nullpunktet ved å løse likningen #f(x)=0#. Det gjør vi slik:

#f(x)=0#

#1,4x-4,9=0#

#x=\frac{4,9}{1,4}#

#\dunderline{x=3,5}#

Funksjonen #f# har altså nullpunktet #x=3,5#.

For hvert steg i utregningen ovenfor manipulerte vi likningen slik at vi for hvert steg kom nærmere svaret. Vi gikk analytisk til verks og vurderte hva som var riktig metode for å finne verdien til #x#. Å programmere datamaskinen din til å gjøre slike analytiske vurderinger er ikke lett. I stedet benytter vi den egenskapen som datamaskiner er best på – den kan gjøre veldig mange utregninger på kort tid.

Når vi skal finne nullpunkter numerisk kan vi forenklet si at vi lar datamaskinen velge en #x#-verdi og regne ut hva funksjonsverdien blir. Hvis dette svaret ikke er nært nok null, lar vi datamaskinen velge en ny verdi for #x#. Slik fortsetter vi helt til vi finner en #x#-verdi som er god nok.

Dersom vi lar datamaskinen velge #x#-verdier helt tilfeldig, blir ikke programmet vårt veldig effektivt for å finne nullpunkter. Derfor bør vi sørge for at #x-#verdiene blir nærmere og nærmere nullpunktet.

En metode for å nærme seg nullpunktet systematisk er halveringsmetoden. Da starter vi med å velge to verdier, #x=a# og #x=b#, på en slik måte at vi er helt sikker på at #f(a)# og #f(b)# ligger på hver sin side av nullpunktet. Det kan vi sjekke ved at #f(a)# og #f(b)# har motsatt fortegn. Da må nullpunktet ligger et sted mellom #a# og #b#.

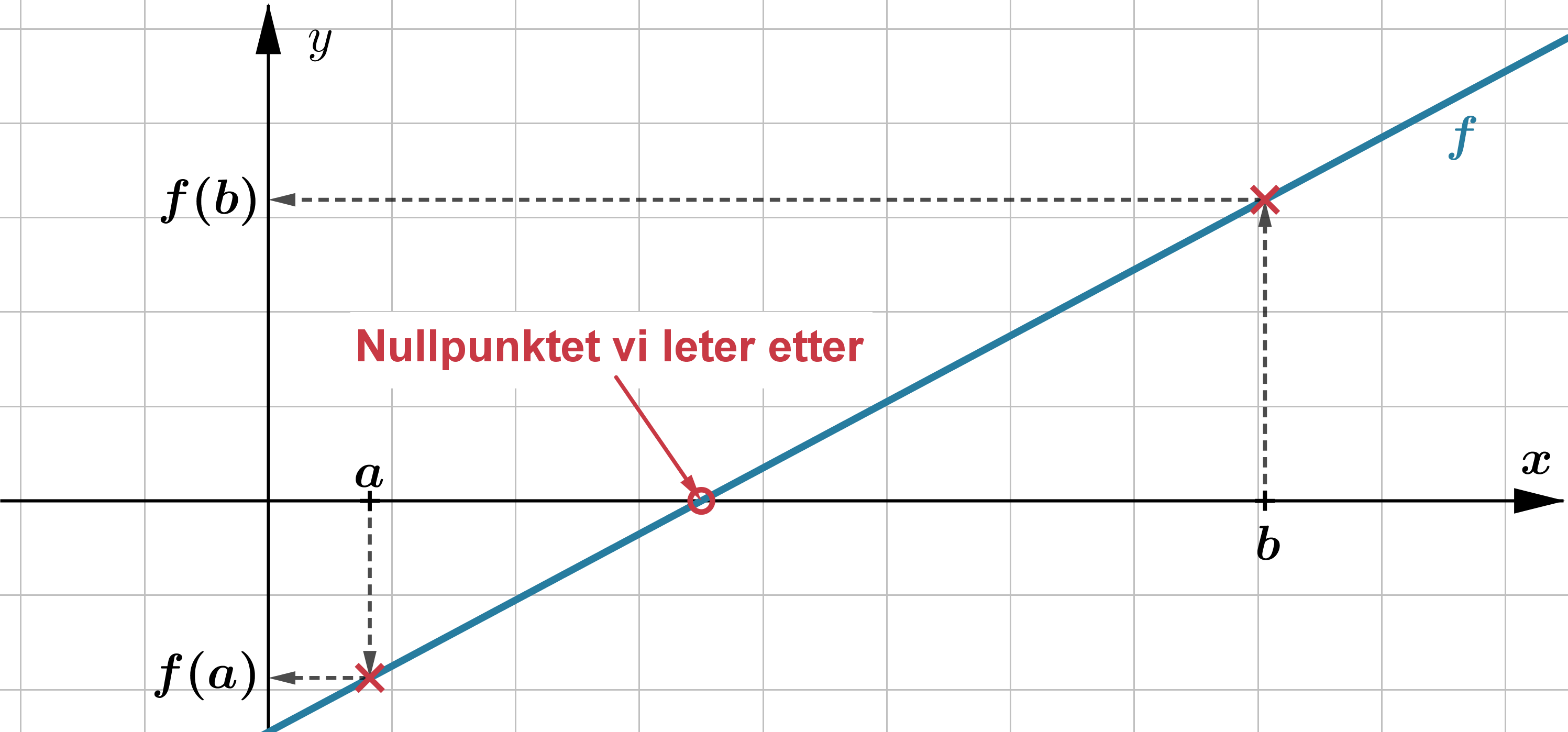
I fortsettelsen her antar vi at det er #f(a)# som er negativ, og at #f(b)# derfor er positiv. Men prinsippet er det samme dersom vi hadde antatt det motsatte. For å nærme oss svaret finner vi midtpunktet #x = m#, som ligger midt mellom #a# og #b#. Verdien til #f(m)# er nå enten negativ, eller så er den ikke det (altså enten lik null eller positiv). Hvis #f(m)# er negativ kan vi bytte ut verdien til #a# med #m#, og i motsatt tilfelle kan vi la verdien #m# bli vår nye #b#.

På figuren nedenfor er midtpunktet #m# slik at #f(m)# positiv. I dette tilfellet vil vi at koden vår skal sette # b = m# før neste steg i løkken.

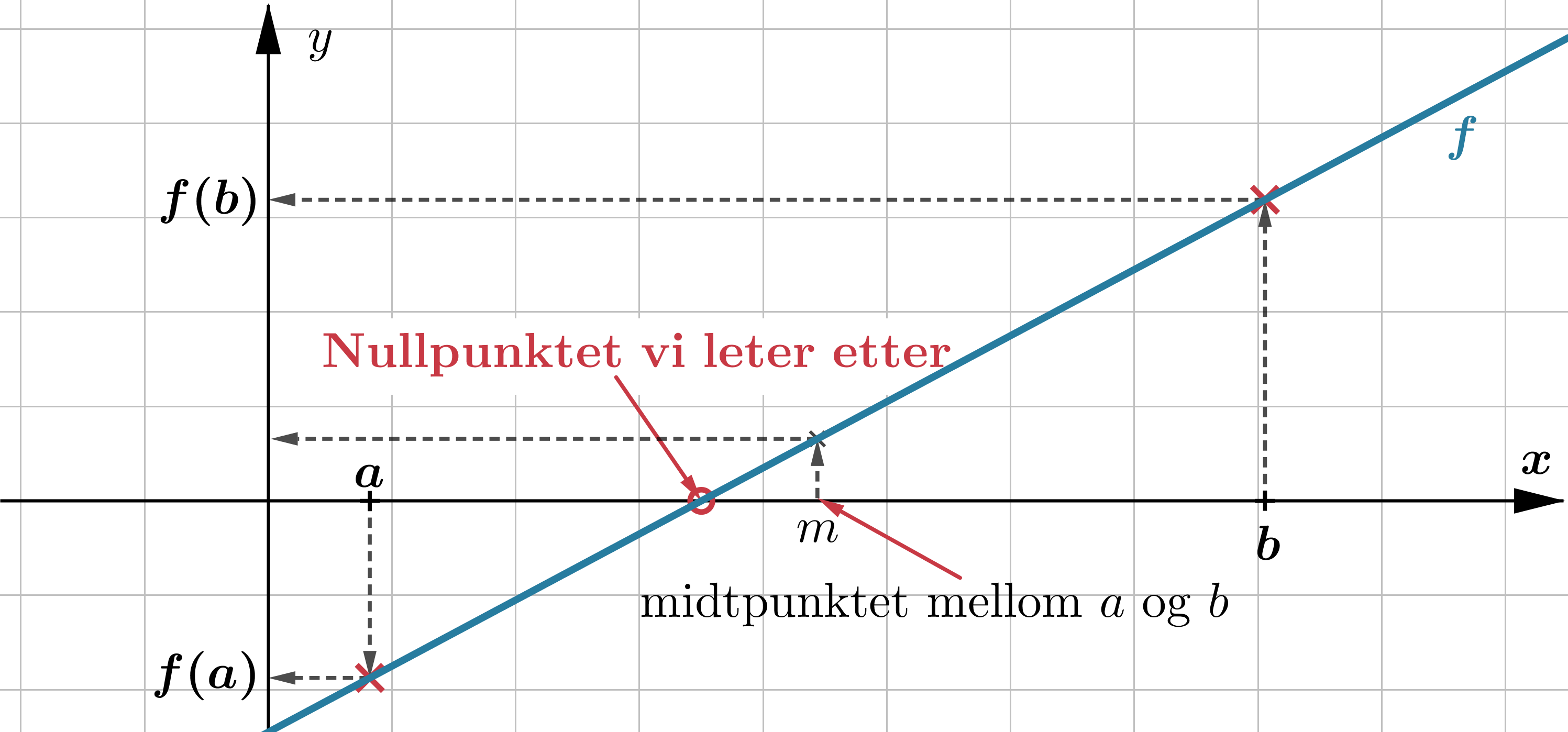
Vi gjentar så disse stegene helt til vi verdien #m# er nær nok nullpunktet vi leter etter. Vi kan forklare algoritmen med pseudokode slik:

#\texttt{a = x-verdi slik at f(a) < 0}#
#\texttt{b = x-verdi slik at f(b) > 0}#
#\texttt{m = midtpunktet mellom a og b: (a+b)/2}#
#\texttt{så lenge f(m) ikke er nærme nok null:}#
#\quad \quad \texttt{hvis f(m) < 0:}#
#\quad \quad \quad \quad \texttt{a = m}#
#\quad \quad \texttt{ellers}#
#\quad \quad \quad \quad \texttt{b = m}#
#\quad \quad \texttt{m = (a+b)/2}#
#\texttt{ferdig! skriv ut svaret x = m.}#

Vi viser denne algoritmen med et eksempel.

La oss legge til en linje i eksempelet ovenfor for å se hvordan koden fungerer. Vi legger til linjen #\texttt{print(m)}# inne i while-løkken slik at programmet skriver ut verdien av midtpunktet #\texttt{m}# for hver repetisjon av løkken.

Da blir koden og resultatet slik som nedefor.

Vi ser at verdien for #\texttt{m}# blir stadig bedre og at koden gjør 18 repetisjoner før nullpunktet er funnet med 5 desimaler nøyaktighet.

De første stegene i koden er slik:

Først blir #m = 5,0#. Det er fordi #a=0# og #b=10#, slik at

#m=\frac{a+b}{2}=\frac{0+10}{2}=5#

Siden #f(m)=f(5)# ikke er negativt (#f(5)=2,1#), blir #b# satt lik 5,0 før neste runde i løkken. Ettersom #a# fortsatt er lik #0# og #b# nå er #5,0# blir andre linje i resultatet #m = 2,5#. Da blir #f(2,5)=-1,4#, som er negativt, og det er nå #a# som settes lik #2,5#. I neste runde gir det #m = 3,75#.

Slik fortsetter koden å gi oss en stadig bedre verdi for nullpunktet. Vi ser av den neste siste linja at #m=3,500022888…# før den siste linja i #\texttt{while}#-løkka gjør at #m# regnes ut enda gang. Det gjør at nullpunktet blir riktig med 5 desimaler. Da avsluttes løkken og svaret skrives ut. Avrundet med fem desimaler er det #x=3,5#.