Å finne nullpunkter til en funksjon er en viktig del av matematikken. Nå skal vi lære å finne nullpunkter ved å bruke kode. Vi tar utgangspunkt i funksjonen:

#f(x)=1,4x-4,9#

Du har sikkert lært å finne nullpunktet ved å løse likningen #f(x)=0#. Det gjør vi slik:

Funksjonen #f# har altså nullpunktet #x=3,5#.

For hvert steg i eksemplet manipulerte vi likningen slik at vi for hvert steg kom nærmere svaret. Vi gikk analytisk til verks og vurderte hva som var riktig metode for å finne verdien til #x#. Å lage programmer som gjøre slike analytiske vurderinger er ikke lett. Men systemer slik som CAS (Computer Algebra System) kan gjøre slikt.

Vi skal heller fokusere på den egenskapen som datamaskiner er best på – den kan gjøre veldig mange utregninger på kort tid.

Når vi skal finne nullpunkter numerisk kan vi forenklet si at vi lar datamaskinen velge en #x#-verdi og regne ut hva funksjonsverdien blir. Hvis dette svaret ikke er nært nok null, lar vi datamaskinen velge en ny verdi for #x#. Slik fortsetter vi helt til vi finner en #x#-verdi som er god nok.

Dersom vi lar datamaskinen velge #x#-verdier helt tilfeldig, blir ikke programmet vårt veldig effektivt for å finne nullpunkter. Derfor bør vi sørge for at #x-#verdiene blir nærmere og nærmere nullpunktet.

En metode for å nærme seg nullpunktet systematisk er halveringsmetoden. Da starter vi med å velge to verdier, #x=a# og #x=b#, på en slik måte at vi er helt sikker på at #f(a)# og #f(b)# ligger på hver sin side av nullpunktet. Det kan vi sjekke ved at #f(a)# og #f(b)# har motsatt fortegn. Da må nullpunktet ligger et sted mellom #a# og #b#.

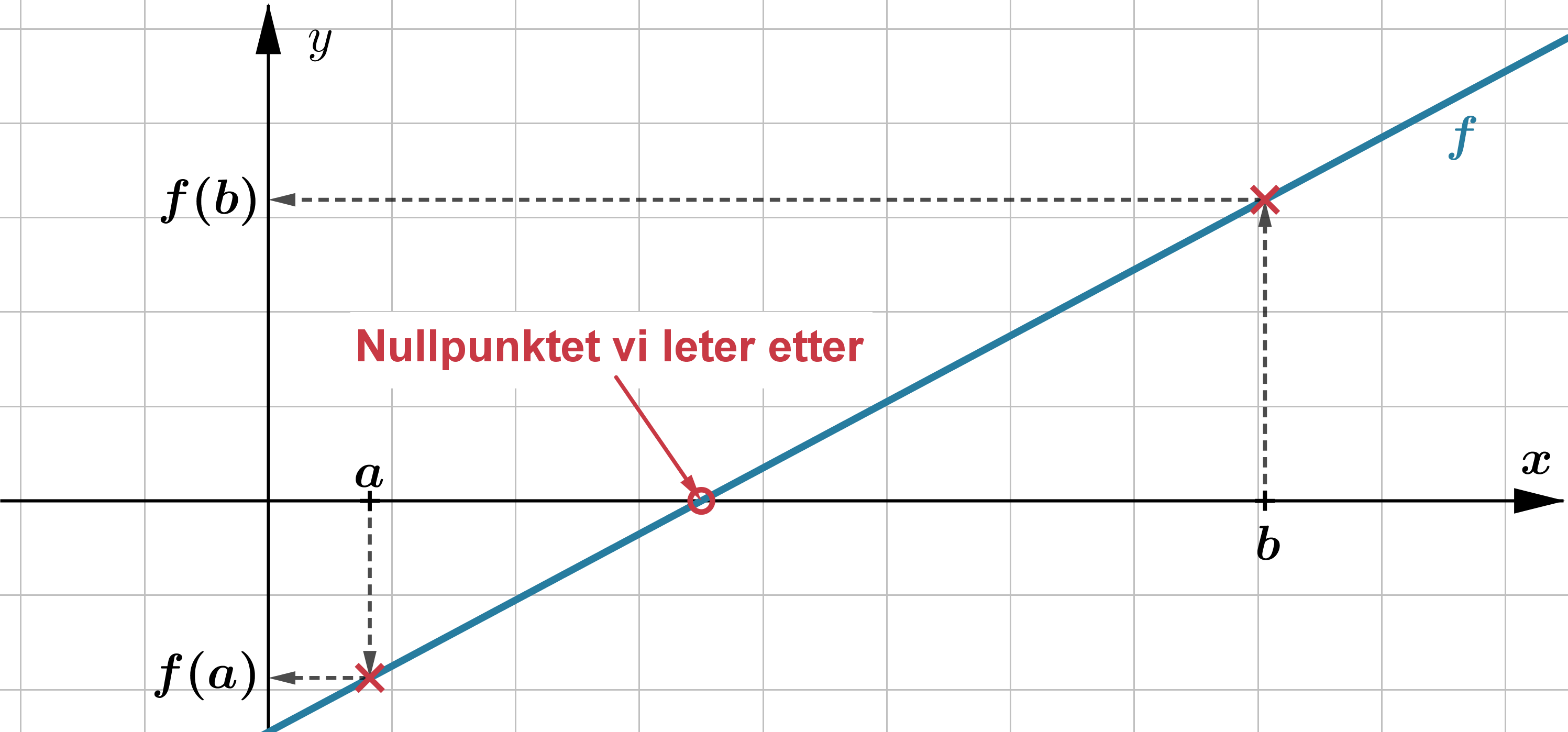
I fortsettelsen her antar vi at det er #f(a)# som er negativ, og at #f(b)# derfor er positiv. Men prinsippet er det samme dersom det motsatte var riktig. For å nærme oss svaret finner vi midtpunktet #x = m#, som ligger midt mellom #a# og #b#. Verdien til #f(m)# er nå enten negativ, eller så er den ikke det (altså enten lik null eller positiv). Hvis #f(m)# er negativ kan vi bytte ut verdien til #a# med #m#, og i motsatt tilfelle kan vi la verdien #m# bli vår nye #b#.

På figuren nedenfor er midtpunktet #m# slik at #f(m)# positiv. I dette tilfellet vil vi at koden vår skal sette # b = m# før neste steg i løkken.

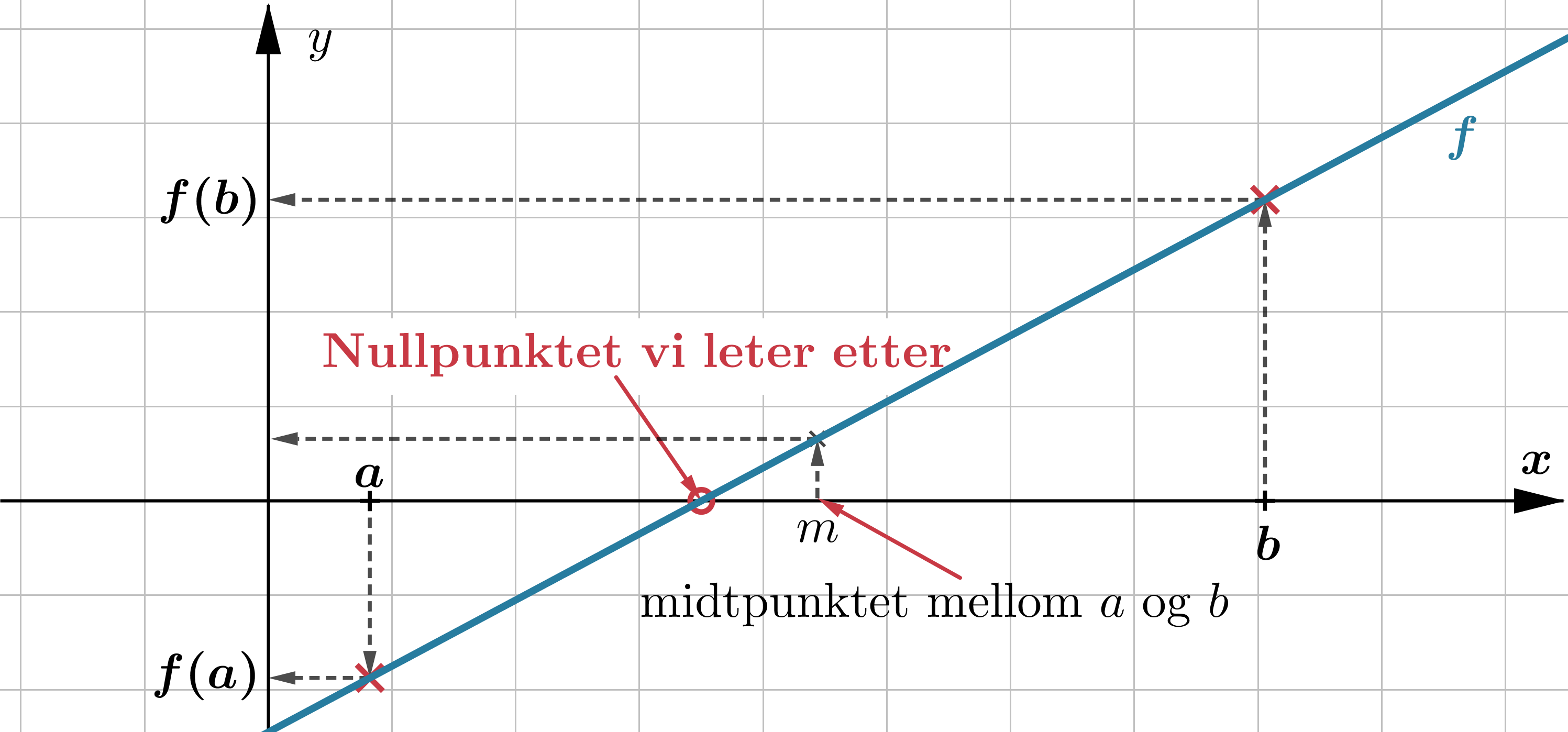
Vi gjentar så disse stegene helt til vi verdien #m# er nær nok nullpunktet vi leter etter. Vi kan forklare algoritmen med pseudokode slik:

#\texttt{a = x-verdi slik at f(a) < 0}#
#\texttt{b = x-verdi slik at f(b) > 0}#
#\texttt{m = midtpunktet mellom a og b: (a+b)/2}#
#\texttt{så lenge f(m) ikke er nærme nok null:}#
#\quad \quad \texttt{hvis f(m) < 0:}#
#\quad \quad \quad \quad \texttt{a = m}#
#\quad \quad \texttt{ellers}#
#\quad \quad \quad \quad \texttt{b = m}#
#\quad \quad \texttt{m = (a+b)/2}#
#\texttt{skriv ut svaret x = m.}#

Vi viser denne algoritmen med et eksempel.